2.5 KiB
ECOMMS Homework 3 - Aidan Sharpe
Problem 1
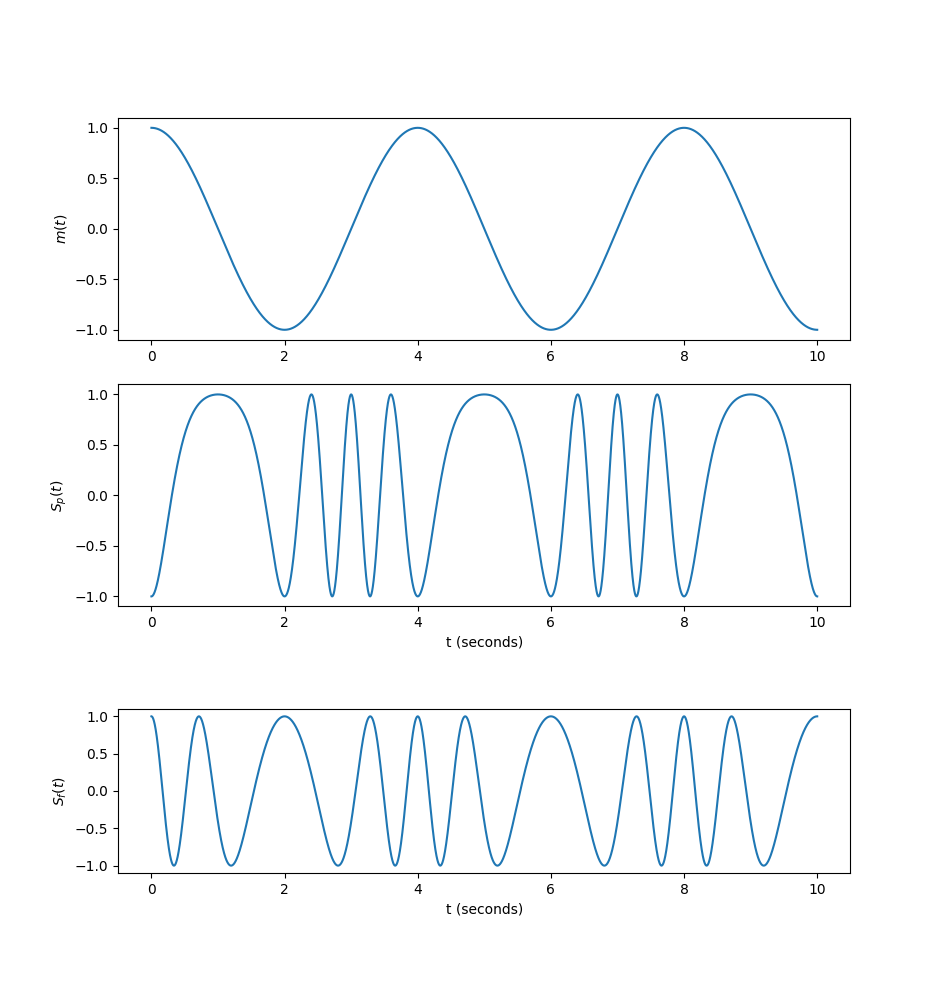
A sinusoidal signal m(t) = \cos(2\pi f_m t) is the input to an angle-modulated transmitter, A_c = 1, and the carrier frequency is f_c = 1 Hz and f_m = f_c/4. Plot m(t), and the corresponding phase and frequency modulated signals, S_p(t) and S_f(t) respecively. D_p = \pi and D_f = \pi.
f_c = 1
f_m = f_c/4
f_s = 8E3
T_s = 1/f_s
A_c = 1
D_p = np.pi
D_f = np.pi
omega_m = 2*np.pi*f_m
omega_c = 2*np.pi*f_c
# Time samples from to 10 seconds with a sampling frequency of 8kHz.
t = np.arange(0,10,T_s)
# The message signal
m = np.cos(omega_m * t)
# The phase modulated signal
S_p = np.cos(omega_c*t + D_p*m)
# The time integral of the mesage signal
M = np.sin(omega_m * t) / omega_m
# The frequency modulated signal
S_f = np.cos(omega_c*t + D_f*M)
Problem 2
An FM signal has sinusoidal modulation with a frequency of $f_m = 15$kHz and a modulation index of \beta = 2.0. Find the transmission bandwidth by using Carson's rule, and find the percentage of total FM signal power that lies within the Carson rule bandwidth.
# Modulation index
beta = 2.0
# Message frequency
f_m = 15E+3
# Transmission bandwidth
B_T = 2*(beta+1)*f_m
\boxed{B_T = 90\text{kHz}}
A_c = 1
n = np.arange(-3,4,1)
# Evaluate the Bessel function at values in Carson rule bandwidth
bessel_values = np.abs(sp.special.jv(n,beta))
P_C = 0.5 * A_c**2 * np.sum(bessel_values**2))
P = 0.5 * A_c**2
\boxed{P_c = 0.9976 P}
Problem 3
A modulated RF waveform is given by 500\cos(\omega_c t + 20\cos(\omega_1 t)), where \omega_1 = 2\pi f_1, $f_1 = 1$kHz, \omega_c = 2\pi f_c, and $f_c = 100$MHz.
3a
If the phase sensitivity D_p = 100 rad/V, find the mathematical expression for the corresponding phase modulation voltage m(t). What is its peak value and frequency?
m(t) = \frac{20\cos(\omega_1 t)}{D_p} = 0.2\cos(\omega_1 t)
Peak value: 2 \times 10^{-1}
Frequency: 1kHz
3b
If the frequency deviation constant $D_f = 10^6$rad/Vs, find the mathematical expression for the corresponding FM voltage m(t). What is its peak value and its frequency?
\theta(t) = 20\cos(\omega_1 t)
m(t) = \frac{1}{D_f} \frac{d \theta(t)}{dt} = -2 \times 10^{-5} \omega_1 \sin(\omega_1 t)
Peak value: 2 \times 10^{-5}
Frequency: 1kHz
3c
If the RF waveform appears across a 50$\Omega$ load, determine the average power and the PEP.
The average power and the PEP are the same: $\frac{A_c^2}{2} \times \frac{1}{50} = 2.5$kW.