3.4 KiB
VLSI Homework 1 - Aidan Sharpe
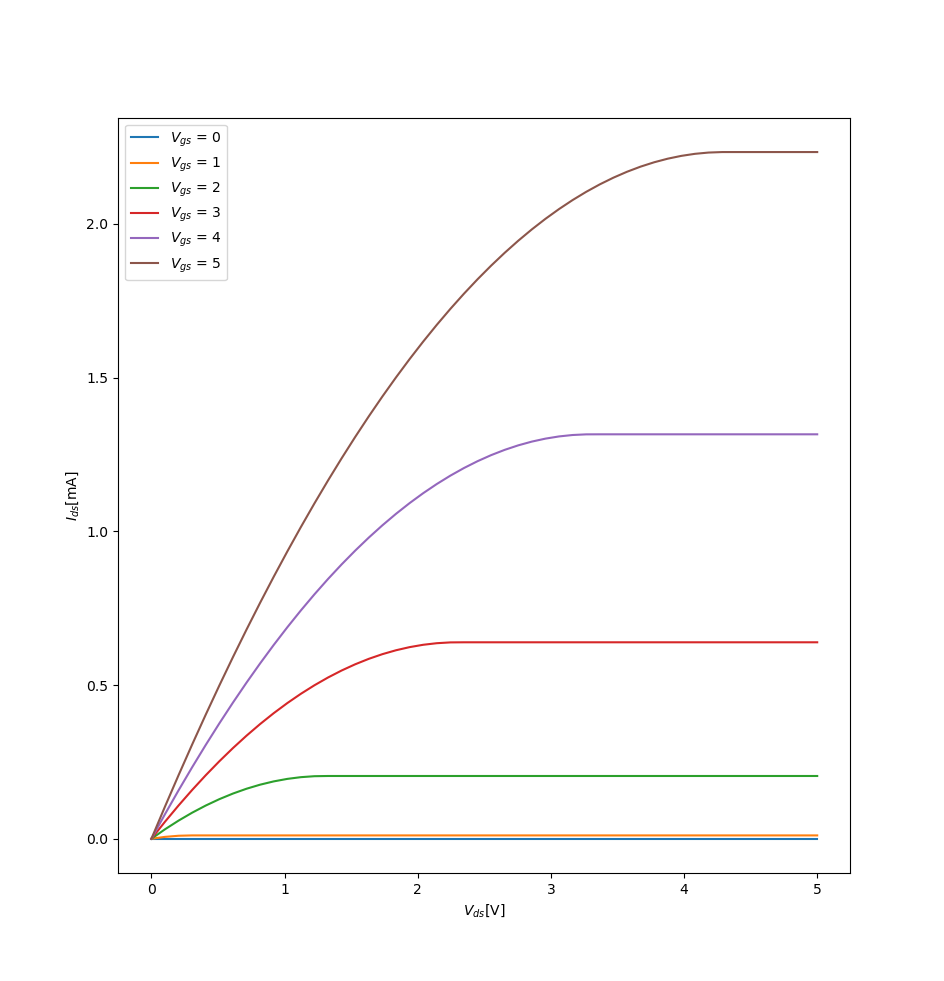
Problem 1
import numpy as np
import matplotlib.pyplot as plt
e_0 = 8.85E-14
k_ox = 3.9
e_ox = e_0 * k_ox
mu = 350 # 350 cm^2 / (V*s)
t_ox = 100E-8 # 100A
C_ox = e_ox / t_ox
W = 1.2
L = 0.6
beta = mu * C_ox * W/L
V_g_range = np.arange(6)
V_t = 0.7
V_dd = np.linspace(0, 5, 50)
def I_ds(V_gs, V_ds, V_t, beta):
if V_gs < V_t:
return np.zeros_like(V_ds)
V_dsat = V_gs - V_t
return np.where(V_ds < V_dsat,
beta * (V_gs - V_t - V_ds/2) * V_ds,
beta * (V_gs - V_t)**2 / 2)
for V_s in (0, 2):
for V_g in V_g_range:
V_gs = V_g - V_s
V_ds = V_dd - V_s
plt.plot(V_ds,
1000*I_ds(V_gs, V_ds, V_t, beta),
label="$V_{gs}$ = "+str(V_gs))
plt.xlabel("$V_{ds}$[V]")
plt.ylabel("$I_{ds}$[mA]")
plt.legend()
plt.show()
Problem 2
Show that a MOSFET with channel length 2L, when operating in the linear region, has the same current I_{DS1} as two MOSFETs in series each with channel length L. Assume the same gate voltage V_{DD} for all MOSFETs in the design and the same supply voltage V_{DS} for both designs.
Known
The current through a MOSFET in the linear region is:
I_{DS} = \beta\left(V_{GS} - V_t - \frac{V_{DS}}{2}\right)V_{DS}The parameter \beta is defined as:
\beta = \mu C_\text{ox} \frac{W}{L}Defining Variables
The factor \beta_1 for the singular MOSFET is \mu C_\text{ox} \frac{W}{2L}, and the factor \beta_2 for each of the MOSFETs in series is \mu C_\text{ox} \frac{W}{L}. Therefore, \beta_2 = 2\beta_1.
The current I_{DS1} through the singular MOSFET is:
I_{DS1} = \beta_1\left(V_{DD} - V_t - \frac{V_{DS}}{2}\right)V_{DS}The current I_{DS2} through both MOSFETs in series is both:
I_{DS2} = \beta_2\left(V_{DD} - V_1 - V_t - \frac{V_{DS} - V_1}{2}\right)(V_{DS} - V_1)I_{DS2} = \beta_2\left(V_{DD} - V_t - \frac{V_1}{2}\right)V_1Expanding I_{DS2}
The first equation for I_{DS2} can be rewritten as the difference of two terms:
I_{DS2} = \beta_2\left(V_{DD} - V_t - \frac{V_{DS}}{2} - \frac{V_1}{2}\right)(V_{DS} - V_1)I_{DS2} = \beta_2\left(V_{DD} - V_t - \frac{V_{DS}}{2} - \frac{V_1}{2}\right)V_{DS} - \beta_2\left( V_{DD} - V_t - \frac{V_{DS}}{2} - \frac{V_1}{2}\right)V_1The term -\frac{V_1 V_{DS}}{2} can be pulled out of the first term, and its complement can be pulled out of the second term. Therefore, I_{DS2} can be simplified to the difference of two terms each in the form of the current through a MOSFET in the linear region.
I_{DS2} = \beta_2\left(V_{DD} - V_t - \frac{V_{DS}}{2}\right)V_{DS} - \beta_2\left( V_{DD} - V_t - \frac{V_1}{2}\right)V_1Reducing I_{DS2}
Notice that the second term is the inverse of the second equation for I_{DS2} under "Defining Variables". Setting them equal:
I_{DS2} = \beta_2\left(V_{DD} - V_t - \frac{V_{DS}}{2}\right)V_{DS} - \beta_2\left( V_{DD} - V_t - \frac{V_1}{2}\right)V_1 = \beta_2\left(V_{DD} - V_t - \frac{V_1}{2}\right)V_1Therefore:
\beta_2\left(V_{DD} -V_t - \frac{V_{DS}}{2}\right)V_{DS} = 2\beta_2\left(V_{DD} - V_t - \frac{V_1}{2}\right)V_1Substituting \beta_2 on the left for 2\beta_1 gives:
2\beta_1\left(V_{DD} - V_t - \frac{V_{DS}}{2}\right)V_{DS} = 2\beta_2\left(V_{DD} - V_t - \frac{V_1}{2}\right)V_1Therefore:
2I_{DS1} = 2I_{DS2}\boxed{I_{DS1} = I_{DS2}}