Rowan-Classes/8th-Semester-Spring-2025/weapon-systems/homework/lecture-5.md

title	author	date	geometry
Lecture 5 Homework	Aidan Sharpe	February 24th, 2025	margin=1in

1.1 What are the individual principles used to create a balanced weapon system?

The weapon system should be robust, simple, and predictable.

1.2 Name three of the measures of weapon effectiveness.

Weapon systems may be measured in terms of circular error probability (\text{CEP}_\text{XX}), probability of mission kill (P_\text{MK}), probability of guidance (P_G), and probability of hit, damage, or kill (P_H, P_D, P_K).

1.3 Is the ENU coordinate system in invariant?

No, because all three directions (East, North, and up) are dependent on where on the surface you are.

1.4 Assume only one illuminator and one launcher in the combat system, what two limitations of the combat system determine the depth of fire?

With only one illuminator, only one semi-active missle can be supported at a time. With only one launcher, the time between firings is limited by the the launchers minimum time between missile launches (\Delta T_{L_\text{min}}).

1.5 What are the two main philosophies in weapon scheduling? How are they different?

Quickdraw

Shoot early and often to maximize the number of shot opportunities.

Sharpshooter

Maximize the performance of every shot by trading firing rate for shot quality.

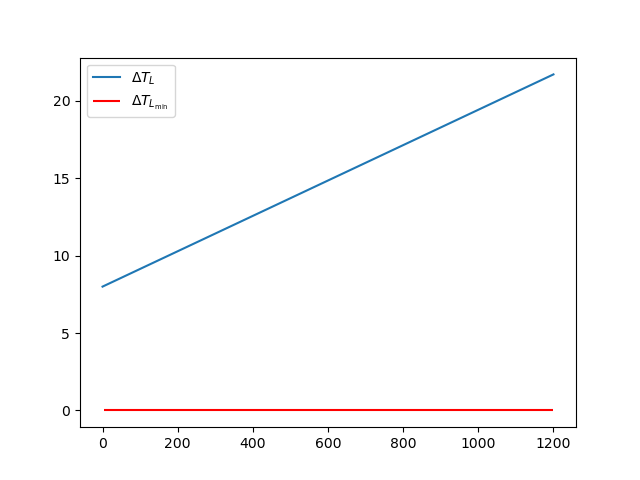
2.1 Delay between missile launches (\Delta T_L)

\Delta T_L = T_H \left(1 + \frac{v_t}{v_m}\right)

import numpy as np
import matplotlib.pyplot as plt


MIN_DELAY = 5
T_HOMING = 8
V_MISSILE = 700


def launch_delay(t_homing, v_missile, v_target):
    return t_homing*(1 + v_target/v_missile)


def main():
    # Range of target speeds from 0 to 1200 (inclusive)
    v_target = np.arange(1200+1)

    # Delta T_L for each target speed
    delays = launch_delay(T_HOMING, V_MISSILE, v_target)

    plt.plot(v_target, delays, label=r"$\Delta T_L$")
    plt.hlines(0, v_target[-1], MIN_DELAY,
	      label=r"$\Delta T_{L_\text{min}}$", color='r')
    plt.legend()
    plt.savefig("launch-delay.png")
    plt.show()

Since the homing time is longer than the minimum time between missile launches, there is no such target speed where \Delta T_{L_\text{Min}} = \Delta T_L.

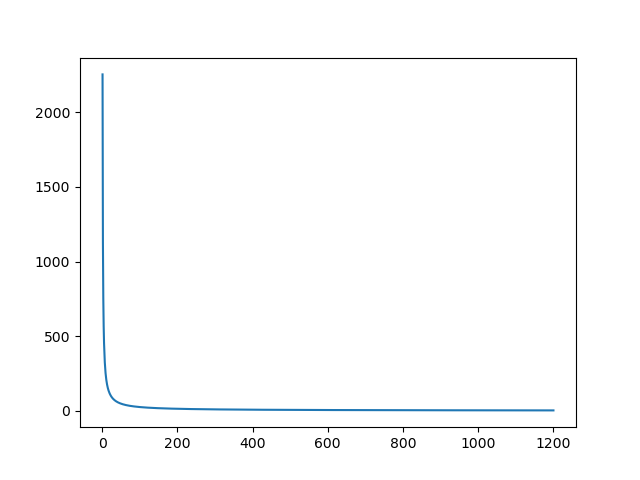
2.2 Depth of Fire

\text{TET} = \frac{\text{ROF} - R_\text{min}}{V_T}

\text{TOF}_1 = \frac{\text{ROF}}{V_M + V_T}

\text{DOF} = \frac{\text{TET} + \text{TOF}_1}{T_H} + 1

import numpy as np
import matplotlib.pyplot as plt

TARGET_RANGE = 20E3
MIN_RANGE = 2E3
MIN_DELAY = 5
T_HOMING = 8
V_MISSILE = 700

def depth_of_fire(target_range, min_range, t_homing, v_target, v_missile):
    t_engagement = (target_range - min_range) / v_target
    t_flight = target_range / (v_missile + v_target)
    return (t_engagement + t_flight)/t_homing

def main():
    # Range of target speeds from 0 to 1200 (inclusive)
    v_target = np.arange(1200+1)
    
    dof = depth_of_fire(TARGET_RANGE, MIN_RANGE, T_HOMING, v_target, V_MISSILE)
    print("DOF for V_T=200:", depth_of_fire(TARGET_RANGE, \
    	 MIN_RANGE, T_HOMING, 200, V_MISSILE))

    plt.plot(v_target, dof, label="Depth of Fire")
    plt.savefig("depth-of-fire.png")
    plt.show()

DOF, where $V_T = 200$[m/s] is 14.0278 shots.