Rowan-Classes/5th-Semester-Fall-2023/Signals-and-Systems/Notes/Chapter1.md

Chapter 1 - Continuous Time Signals

Continuous Time Signal

A continuous time signal is a function x(t) that maps values from \Reals to \Reals or \Complex.

Causal Signals

A signal, x(t), is said to be causal if it has value 0 for t<0.

Non-causal Signals

A signal, x(t), is said to be non-causal, or not causal, if x(t) is not 0 for all t<0.

Finite Support

A signal, x(t), is said to have finite support, or finite duration, if there exists inputs T_1 and T_2 such that x(t) = 0 for t < T_1 and t > T_2.

Infinite Support

A signal, x(t), is said to have infinite support, or infinite duration, if it does not have infinite support.

There are three types of inifinite support:

1. Right-sided: the signal has domain (T_1, +\infty)
2. Left-sided: the signal has domain (-\infty, T_2)
3. Two-sided: the signal has domain (-\infty, +\infty)

1.1 Basic Signal Operations

Signal Addition

Signal addition is of the form: z(t) = x(t) + y(t), where the amplitude of the signal z(t) is the net amplitude of x(t) and y(t).

Scalar Multiplication

Scalar multiplication is of the form: z(t)=\alpha x(t). The amplitude of the output is proportional to \alpha.

Time Shift

A time shift is of the form: z(t)=x(t-\tau). When \tau > 0, the time shift is said to be a delay. When \tau < 0, the time shift is said to be an advance.

Time Scale

A time scale is of the form: z(t)=x(at). For \lvert a \rvert > 1, the scaling is said to be a compression. For \lvert a \rvert < 1, the scaling is said to be an expansion. For a < 0, a time reflection over t=0 occurs.

Figure 1.1.1 - Signal Transformations

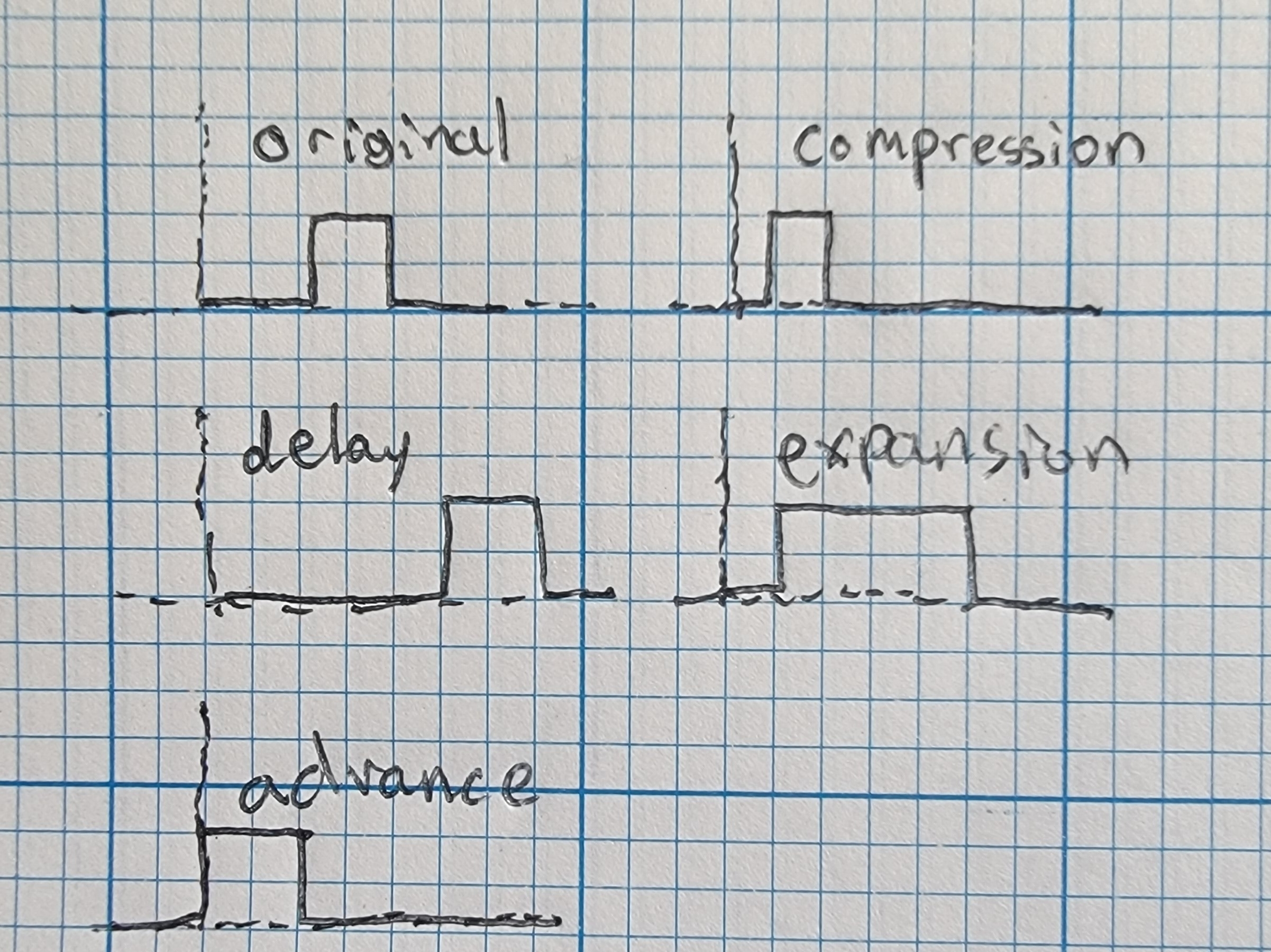
Figure 1.1.2 - Signal Combinations

1.2 Combinations of Operations

Review of Reflections

Every t becomes a -t.

x(t) = \begin{cases} t & 0 \leq t \leq 8 \\ 0 & otherwise \\ \end{cases}

Example 1

x(t) = \begin{cases} t & 0 \leq t \leq 8 \\ 0 & otherwise \\ \end{cases}

How to find y(t) = x(at - b)

Method 1 (recommended)

1. Find v(t) = x(t-b)
2. Find w(t) = v(\lvert a \rvert t) = x( \lvert a \rvert t - b)
3. If a \gt 0, then \lvert a \rvert = a. y(t) = w(t) = x(at - b)
4. If a \lt 0, then \lvert a \rvert = a. y(t) = w(-t) = x(-\lvert a \rvert t - b)

Method 2

1. Find v(t) = x(\lvert a \rvert t)
2. Find w(t) = v(t - \frac{b}{\lvert a \rvert}) = x(\lvert a \rvert \left(t - \frac{b}{\lvert a \rvert} \right))

Example

Find x(3t-5)

Lecture 5

The Impulse Function

\delta(t) = \begin{cases} 0 & t \ne 0 \\ \infty & t = 0 \\ \end{cases}

\int_{-\infty}^{\infty} \delta(t) dt = 1

\delta(t - \alpha) = \begin{cases} \infty & t=\alpha \\ 0 & t \ne \alpha \\ \end{cases}

\delta(2t - 3) = \begin{cases} \infty & 2t-3=0, t=3/2 \\ 0 & t \ne 3/2 \end{cases}

Properties

f(t) \delta(t- \alpha) = f(\alpha) \delta(t-\alpha)

\int_a^b f(t) \delta(t - \alpha)dt= \begin{cases} f(\alpha) & \alpha \in [a, b] \\ 0 & otherwise \end{cases}

Unit step

u(t) = \begin{cases} 1 & t \ge 0 \\ 0 & t \lt 0 \end{cases}

\delta(t) = \frac{du(t)}{dt}

u(t) = \int_{-\infty}^{t} \delta(\tau)d\tau = \begin{cases} 1 & t \ge 0 \\ 0 & t \lt 0 \end{cases}

u(t - \tau) = \begin{cases} 1 & t \ge \tau \\ 0 & t \lt \tau \end{cases}

u(-t + 5) = \begin{cases} 1 & t \le 5 \\ 0 & t \gt 5 \end{cases}

The difference between u(t) and u(t-1) is a finite support pulse from 0 to 1.

Ramp

r(t) = t u(t) = \begin{cases} t & t \ge 0 \\ 0 & t \lt 0 \end{cases}

\frac{dr(t)}{dt} = \frac{tdu(t)}{dt} + (1)u(t) = t\delta(t) + u(t) = u(t)

Derivatives

1. \cos(2 \pi t)\left[ u(t) - u(t-1) \right] = \begin{cases} 0 & t \lt 0 \\ \cos(2\pi t) & 0 \le t \lt 1 \\ 0 & t \ge 1 \end{cases}

   Using the product rule:

   \cos(2\pi t)\left[ \delta(t) - \delta(t-1) \right] + -\sin(2\pi t)(2\pi)\left[u(t)-u(t-1)\right]

2. u(t) - 2u(t-1) + u(t-2) = \begin{cases} 0 & t \lt 0 \\ 1 & 0 \le t \lt 1 \\ -1 & 1 \le t \lt 2 \\ 0 & t \ge 2 \end{cases}

Energy and Power of Signals

Energy

The energy of a signal x(t) could be finite or infinite.

Given a real or complex signal, x(t), the energy, E_x, is defined as:

E_x = \int_{-\infty}^{\infty} \lvert x(t) \rvert^2 dt

1. If x(t) has finite support, the domain is [a, b], and therefore E_x is a finite integral with bounds a and b.

2. If x(t) has infinite support, E_x is an improper integral and may or may not have finite value.

3. If x(t) is periodic, E_x is infinite.

Power

The power, P_x, of an aperiodic signal is defined as:

P_x = \lim_{T \to \infty} \frac{1}{2T} \int_{-T}^{T} \lvert x(t) \rvert^2 dt

The power, P_x, of a periodic signal with period, T_0, x(t) is defined as:

P_x = \frac{1}{T_0}\int_{t_0}^{t_0 + T_0} \lvert x(t) \rvert^2 dt

The most convenient starting times, t_0 are -\frac{T_0}{2} and 0. The bounds of integration will be \left[ -\frac{T_0}{2}, \frac{T_0}{2} \right] and \left[ 0, T_0 \right] respectively.

For a periodic signal, the power is the energy of one period normalized by the length of the period.

FACT: A finite energy aperiodic signal has zero power.

P_x = \lim_{T \to \infty} \frac{1}{2T} \int_{-T}^{T} \lvert x(t) \rvert^2 dt

=\lim_{T \to \infty} \frac{1}{2T} [N]

Where N is some finite number.

\lim_{T \to \infty} \frac{N}{2T} = 0

Procedure

1. Determine if x(t) is finite support or infinite support.
   • If finite support: E_x \lt \infty, P_x = 0
2. If x(t) is infinite support, determine periodicity of x(t)
   • If aperiodic, calculate E_x, P_x
   • If periodic: E_x = \infty, calculate P_x

Facts

If:

x(t) = A\cos(\omega_0 t + \theta)

Then:

E_x = \infty

P_x = \frac{A^2}{2}

If:

x(t) = \sum_k A_k\cos(\omega_k t + \theta)

Then:

E_x = \infty

P_x = \sum_k \frac{A_k^2}{2}