1.9 KiB
1.9 KiB
title, author, date, geometry
| title | author | date | geometry |
|---|---|---|---|
| ECE09426 Lecture 6 Homework | Aidan Sharpe | March 3rd, 2025 | margin=1in |
Required PDMS for a HAW System
import numpy as np
import matplotlib.pyplot as plt
P_TX = 7E3
LOSS_TX = 10**(5/10)
GAIN_TX = 10**(35/10)
MAX_RANGE = 60E3
TARGET_AREA = 1
def PDMS(tx_power, tx_gain, radar_cross_section, tx_loss, dist_source_target, dist_target_missile):
tx_p_gain = (tx_power*tx_gain) / (4*np.pi*tx_loss)
p_ref = radar_cross_section / (dist_source_target**2)
p_rx = 1 / (4*np.pi*dist_target_missile**2)
return tx_p_gain * p_ref * p_rx
def main():
pd_min = PDMS(P_TX, GAIN_TX, TARGET_AREA, LOSS_TX, MAX_RANGE, MAX_RANGE)
pd_min_db = 10*np.log10(pd_min)
print(pd_min_db)
PDMS required = -144.6592668956451
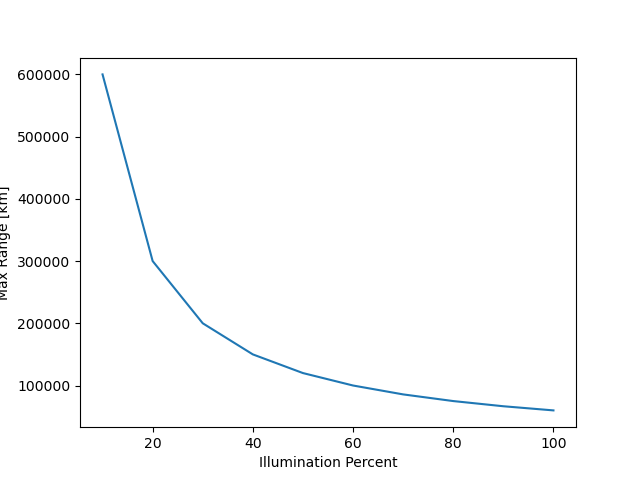
PDMS for a non-HAW System
import numpy as np
import matplotlib.pyplot as plt
MAX_RANGE = 60E3
def main():
illumination_percent = np.arange(0.1, 1.1, 0.1)
max_range = MAX_RANGE/illumination_percent
plt.plot(100*illumination_percent, max_range)
plt.xlabel("Illumination Percent")
plt.ylabel("Max Range [km]")
plt.show()
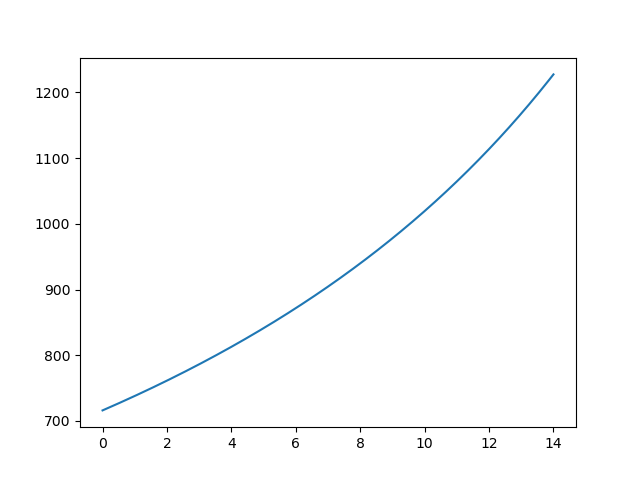
Rocket Motor Math
import numpy as np
import matplotlib.pyplot as plt
g = 9.81
I_SP = 250
BURN_TIME = 14
INITIAL_MASS = 1200
FINAL_MASS = 700
def v_burnout(I_sp, t_burn, w_launch, w_burnout):
return I_sp * g*np.log(w_launch/w_burnout)
def main():
t = np.linspace(0, BURN_TIME, 500)
m_propellant = INITIAL_MASS - FINAL_MASS
w_propellant_0 = g*m_propellant
w_rocket = g*FINAL_MASS
weight_flow_rate = w_propellant_0/BURN_TIME
v_exit = I_sp*g
w_propellant = w_propellant_0 - weight_flow_rate*t
thrust = weight_flow_rate*v_exit*g
w_total = w_rocket + w_propellant
acceleration_g = thrust/w_total
plt.plot(t, acceleration_g)
plt.show()
if __name__ == "__main__":
main()