Homework 5 - Aidan Sharpe

Problem 1

In a binary communication system, let the receiver test statistic of the received signal be r_0. The received signal consists of a polar digital signal plus noise. The polar signal has values s_{01}=A and s_{02}=-A. Assume that the noise has a Laplacian distribution:

f(n_0) = \frac{1}{\sqrt{2} \sigma_0} e^{-\sqrt{2}|n_0|/\sigma_0}

where \sigma_0 is the RMS value of the noise, f(n_0) is the probability density function (PDF), and n_0 is the signal. In the case of a PDF of s_{01} and s_{02}, replace n_0 by r_0-A and r_0+A. The shape of the PDF for s_{01} and s_{02} is the same. Find the probability of error P_e as a function of A/\sigma_0 for the case of equally likely signaling and V_T having the optimum value.

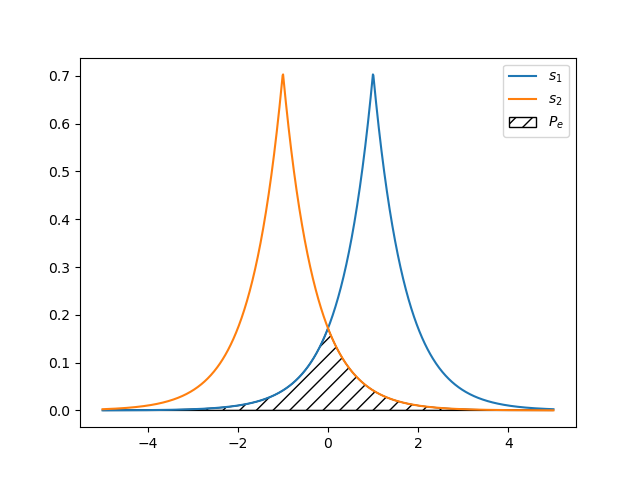
Given the two PDFs corresponding to s_1 and s_2, the probability of a bit error is the same as the area of the intersection of the two PDFs, as seen in figure \ref{error_pdfs}.

$PDFs corresponding to bit error probability \label{error_pdfs}$

The curve traced out by this area is

p(r_0) = \frac{1}{2}\left[f(r_0 | s_1) + f(r_0 | s_2) - \|f(r_0 | s_1) - f(r_0 | s_2) \|\right]

to find the area under the curve (the probability of a bit error P_e), we integrate p(r_0) for all values of r_0. Since f(r_0 | s_1) and f(r_0 | s_2) are PDFs, the area under each must be unity. Therefore, distributing the \frac{1}{2} term, we are left with:

P_e = 1 - \frac{1}{2} \int\limits_{-\infty}^\infty  \left|f(r_0 | s_1) - f(r_0 | s_2)\right| dr_0

Finally, we expand and simplify the integral to:

P_e = 1 - \frac{\sqrt{2}}{4\sigma_0} \int\limits_{-\infty}^\infty  \left|e^{-\sqrt{2} |r_0-A| /\sigma_0} - e^{-\sqrt{2} |r_0 + A|/\sigma_0}\right| dr_0

After evaluating the intergral, we find that P_e = e^{-\sqrt{2}A/\sigma_0}.

Problem 2

A digital signal with white Gaussian noise is received by a receiver with a matched filter. The signal is a unipolar non-return to zero signal with $s_{01}=1$[V] and $s_{02}=0$[V]. The bit rate is 1 Mbps. The power spectral density of the noise is $N_0/2=10^{-8}$[W/Hz]. What is the probability of error P_e? Assume the white Gaussian noise is thermal noise.

For a unipolar signal received by a receiver with a matched filter, the probability of error is given by:

P_e = Q\left(\sqrt{\frac{A^2 T}{4 N_0}}\right)

where A = 1 - 0 = 1 is the amplitude and $T= 1[\mu$s]. Therefore, P_e = 2.03 \times 10^{-4}.

2.4 KiB Raw Blame History

Homework 5 - Aidan Sharpe

Problem 1

Problem 2

2.4 KiB

Raw Blame History